Unsure When a Video or Photo was Taken? How to Tell by Measuring the Length of Shadows

Establishing the time within a video or image can be a difficult and frustrating task for open source researchers. If you’re lucky, you’ll get a brief glance at a wall-clock or wristwatch — but in most cases you won’t. Measuring shadows, however, can help provide a solution.

It’s already well known that it’s possible to use the angle of shadows to assess the time in an image.  SunCalc, a tool which simulates the movement of the sun through the sky on different dates and locations across the Earth, can be used to do this relatively easily. 

However, sometimes the angle of these shadows might not be clear or there may not be sufficient reference points in a video or picture to accurately judge the angle. 

But just as the angle of a shadow can be used to work out the angle of the sun from North (the azimuth), so the relative length of a shadow can be used to work the angle of the sun from the horizon (the altitude).

As the sun rises in the sky, shadows will initially point west and start long before reaching their shortest length at around midday. They will then point east as they gradually lengthen before sunset. This predictable change in length can be used to judge the time.

Importantly, it’s not necessary to know the actual height of the object casting the shadow. What matters is only the proportional length of the shadow compared to the object. This means that the measurements seen in this article bear no relation to the actual heights and lengths of the objects and shadows. But since we’re only interested in their proportions in comparison to each other, this doesn’t matter. 

In order for this technique to work well, the image or video needs to fit several conditions:

1. The location and date of the image must be known
2. The object and its shadow must be roughly at right angles to the camera 
3. The shadow must be cast on a surface level with the horizon (a flat floor)
4. The image should not be overly distorted by camera lenses, such as fish-eye lenses

Finally, when carrying out this technique, it should be noted that shadows will be a particular length twice during a day: once in the morning, once in the afternoon. Therefore it’s important to check the direction of the shadow. 

Example One: Controlled Conditions

In this example I have used a photo I took at the Al Aqsa compound in Jerusalem on 14 October 2019. Let’s apply the shadow by proportional length technique and see what time we calculate.

The Al Aqsa compound in Jerusalem. Photo by Nick Waters.

In this photo a member of the security forces can be seen leaning against a fence. We can see that the picture fits the four conditions:

1. The location and date of the image must be known
2. The object and its shadow must be roughly at right angles to the camera 
3. The shadow must be cast on a surface level with the horizon (a flat floor)
4. The image should not be overly distorted by camera lenses, such as fish-eye lenses

Next, we measure the lengths of the object and shadow within the image. Remember that what is important here is the proportion between these two measurements, rather than the actual measurements themselves. 

The Al Aqsa compound in Jerusalem with shadow measurements added. Photo by Nick Waters.

We then go to Suncalc, set  the location to this spot in the Al Aqsa Compound and input the height of the object as 2.33 metres, which SunCalc refers to as “at an object level”. We then adjust the time until the shadow length is as close as possible to that seen in the image (3.53 m). The SunCalc input process is detailed in the image below.

Suncalc.org calculation of shadow length. Click or tap to see full size image.

This gives us a time of 09:37. After conducting this analysis I checked the EXIF data from my camera and found it had been taken at 09:43, a mere six minute difference.

Example Two: Still From Video

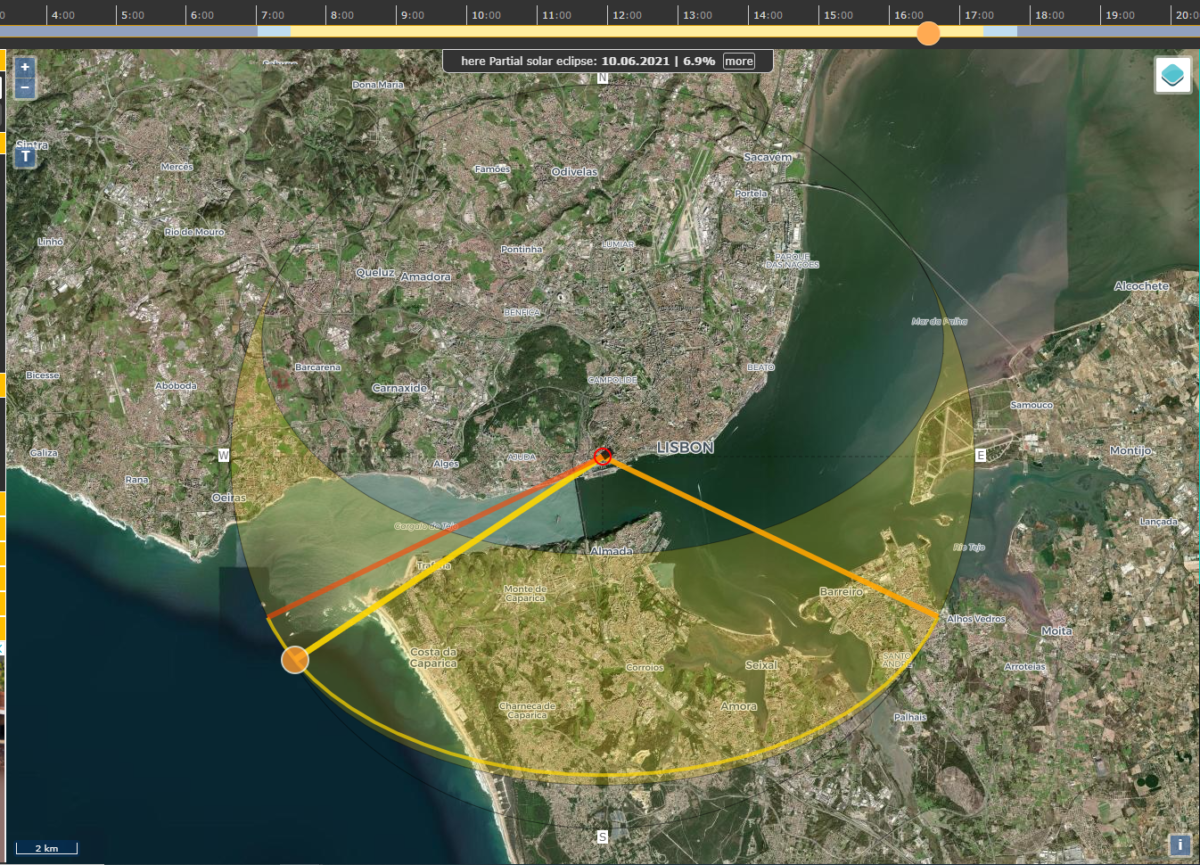
In the example below we see a still from a video showing a group of people watching a Saudi-led coalition airstrike which killed scores of civilians in the town of Zabid, Yemen, on 12 May 2015.

Still image from a video posted by Mohammad al-Hadad.

As we can see, the shadow of the man in the white shirt on the left is being cast on a flat surface at a rough right angle to the camera. We can therefore measure the length of the shadow compared to the length of the object casting it in order to calculate a time. 

In this case, the height of the man in the image was measured as 5.67 centimetres and his shadow, which appears to just stretch past the leg of the man to the right, as 9.84 cm.

Still image from a video posted by Mohammad al-Hadad with shadow measurements added.

Using Suncalc, we then set the “object level” (the height of the object casting the shadow) as 5.67m and change the time until the shadow length shows as close as possible to 9.84m.  This gives us a time of 16:14.

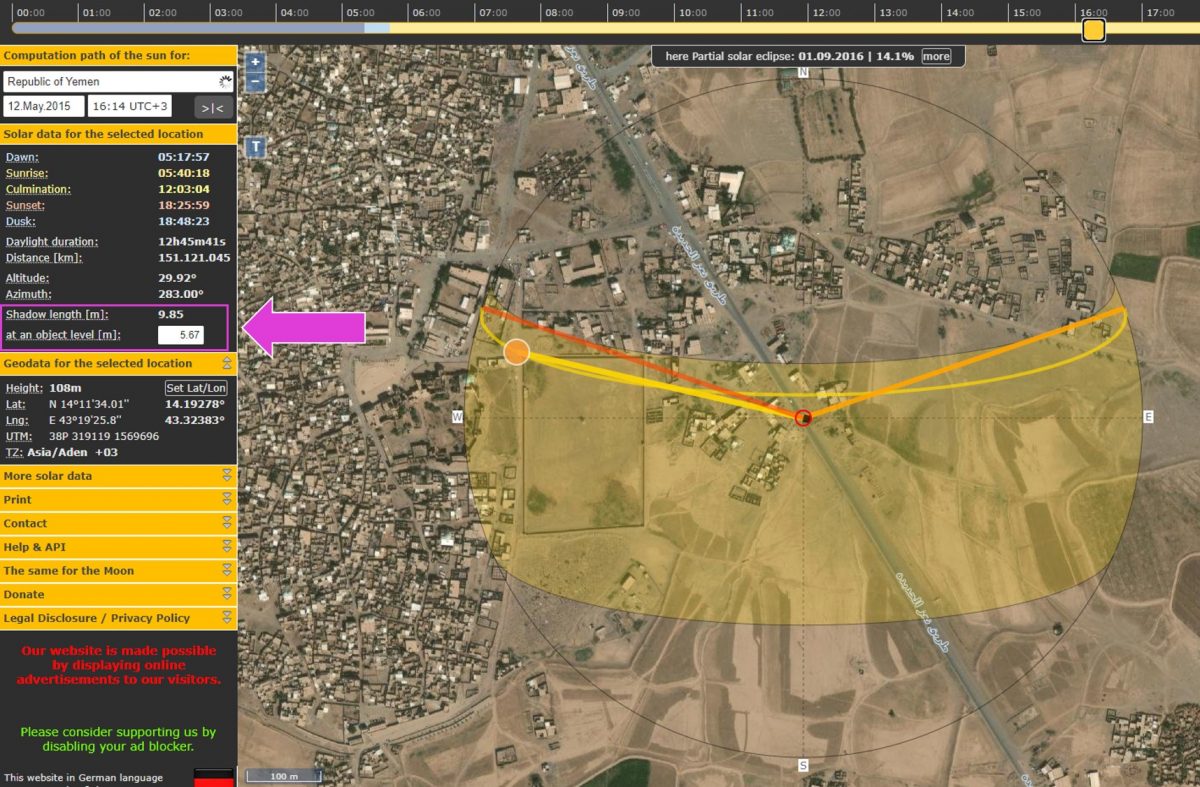
Suncalc.org calculation of shadow length. Click or tap to see full size image.

In order to test the accuracy of the method in this case we can change the time by 15 minutes either side of 16:14 to see what shadow lengths we would get.

• At 16:14 the shadow is 1.74 times the height of the object casting it.
• 15 minutes earlier, at 15:59 the shadow is 1.51 times the height of the object casting it.
• 15 minutes later, at 1629 the shadow is 2.02 times the height of the object casting it. 

Still image from a video posted by Mohammad al-Hadad with shadow measurements added.

As we can see, although the time established by this shadow calculation should be regarded as relatively rough, it is still certainly within a period of 15 minutes either side of 16:14.

When applying this technique it’s often useful to establish a time window in this way, rather than stating a specific time. This can be done quite easily by adjusting the time within SunCalc until the length of the shadow is clearly no longer consistent with the calculation. 

Conclusion

Although this technique is slightly more difficult to apply than judging time by angle of shadow, it can still be useful when there are insufficient reference points to estimate an angle. As long as the correct conditions are met, this technique can be reasonably accurate, sometimes surprisingly so. 

If you’re interested in how SunCalc can also be used for geolocation, we’ve written about this technique here.